Design A Matrix Of Translation With Homogeneous Coordinate System

Here we perform translations rotations scaling to fit the picture into proper position.

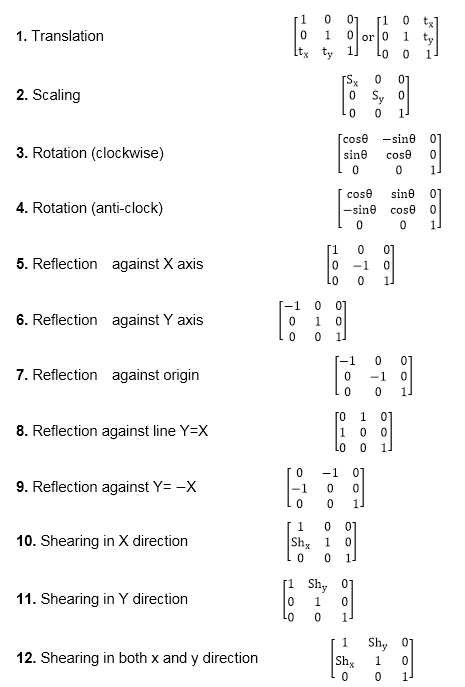
Design a matrix of translation with homogeneous coordinate system.

Translation columns specify the directions of the bodyʼs coordinate axes. The 3x3 matrix a represents scale and rotation the 3d vector t represents translation using homogeneous coordinates all affine transformations are represented with one matrix vector multiplication affine transformations. In mathematics homogeneous coordinates or projective coordinates introduced by august ferdinand möbius in his 1827 work der barycentrische calcul are a system of coordinates used in projective geometry as cartesian coordinates are used in euclidean geometry they have the advantage that the coordinates of points including points at infinity can be represented using finite coordinates. Homogeneous coordinates are generally used in design and construction applications.

The functional form. All ordinary linear transformations are included in the set of. Hand origin basea 1 x 1 a 2 2a 3 x 3a 4 x 4a 5 x 5 hand origin where. It specifies three coordinates with their own translation factor.

In this way we can represent the point by 3 numbers instead of 2 numbers which is called homogenous coordinate system. N 1a n homogeneous transformation matrix which relates the coordinate frame of link n to the coordinate frame of link n 1. Becomes. To convert a 2 2 matrix to 3 3 matrix we have to add an extra dummy coordinate w.

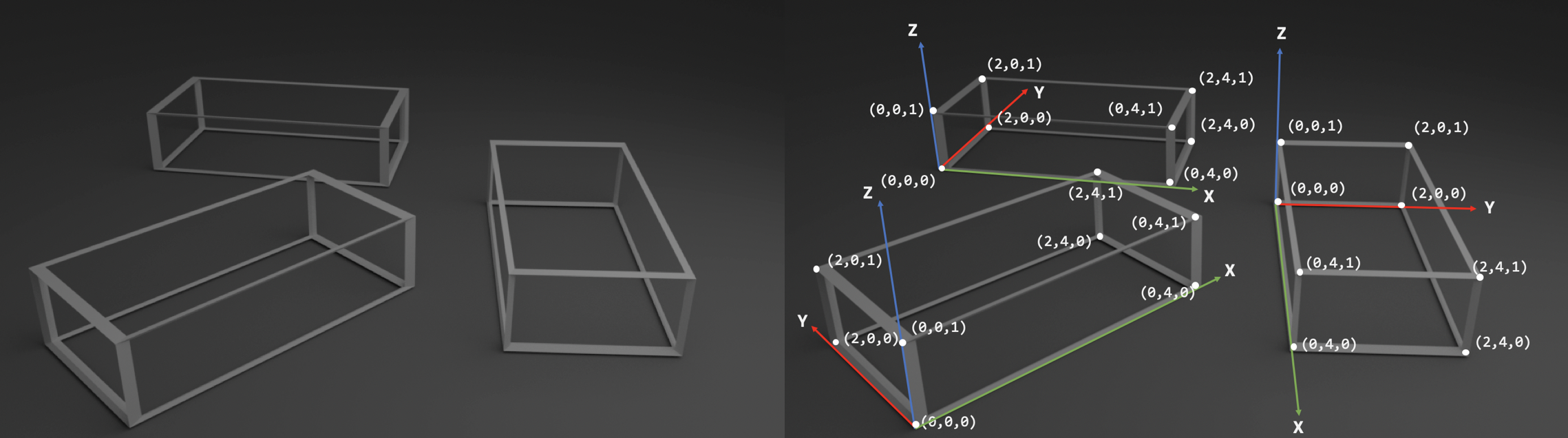
For two dimensional geometric transformation we can choose homogeneous parameter h to any non. Homogeneous coordinates 4 element vectors and 4x4 matrices are necessary to allow treating translation transformations values in 4th column in the same way as any other scale rotation shear transformation values in upper left 3x3 matrix which is not possible with 3 coordinate points and 3 row matrices. Translation three dimensional transformation matrix for translation with homogeneous coordinates is as given below. Like two dimensional transformations an object is translated in three dimensions by transforming each vertex of the object.

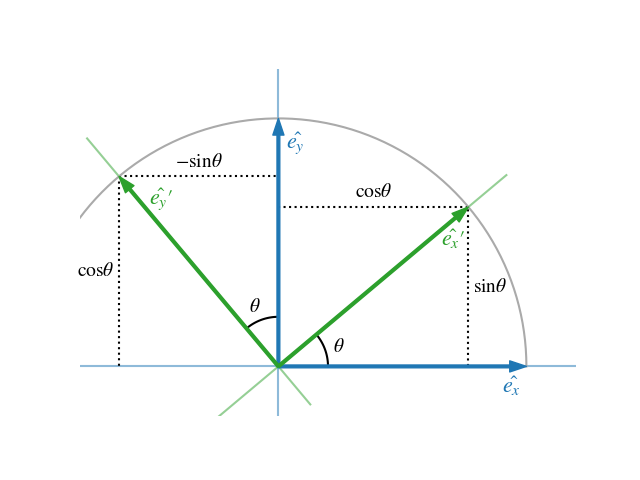
In this system we can represent all the transformation equations in matrix multiplication. Given the u v coordinate of a point p with respect to the second link the x y coordinates of p in the world coordinate system is 1a square matrix qis orthogonalif qqt tq i. Applying a rotation rot θ1 θ2 followed by a translation trans dcosθ1 dsinθ1.